A1. The parallelogram ABCD has AB = a, AD = 1, angle BAD = A, and the triangle ABD has all angles acute. Prove that circles radius 1 and center A, B, C, D cover the parallelogram iff a ≤ cos A + √3 sin A.
A2. Prove that a tetrahedron with just one edge length greater than 1 has volume at most 1/8.
A3. Let k, m, n be natural numbers such that m + k + 1 is a prime greater than n + 1. Let cs = s(s+1). Prove that: (cm+1 - ck)(cm+2 - ck) ... (cm+n - ck)
is divisible by the product c1c2 ... cn.
B1. A0B0C0 and A1B1C1 are acute-angled triangles. Construct the triangle ABC with the largest possible area which is circumscribed about A0B0C0 (BC contains A0, CA contains B0, and AB contains C0) and similar to A1B1C1.
B2. a1, ... , a8 are reals, not all zero. Let cn = a1n + a2n + ... + a8n for n = 1, 2, 3, ... . Given that an infinite number of cn are zero, find all n for which cn is zero.
B3. In a sports contest a total of m medals were awarded over n days. On the first day one medal and 1/7 of the remaining medals were awarded. On the second day two medals and 1/7 of the remaining medals were awarded, and so on. On the last day, the remaining n medals were awarded. How many medals were awarded, and over how many days?
Solutions
Problem A1
The parallelogram ABCD has AB = a, AD = 1, angle BAD = A, and the triangle ABD has all angles acute. Prove that circles radius 1 and center A, B, C, D cover the parallelogram iff
a ≤ cos A + √3 sin A.
Solution
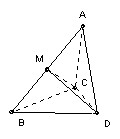
Evidently the parallelogram is a red herring, since the circles cover it iff and only if the three circles center A, B, D cover the triangle ABD.
The three circles radius x and centers the three vertices cover an acute-angled triangle ABD iff x is at least R, the circumradius. The circumcenter O is a distance R from each vertex, so the condition is clearly necessary. If the midpoints of BD, DA, AB are P, Q, R, then the circle center A, radius R covers the quadrilateral AQOR, the circle center B, radius R covers the quadrilateral BROP, and the circle center D radius R covers the quadrilateral DPOQ, so the condition is also sufficient.
We need an expression for R in terms of a and A. We can express BD two ways: 2R sin A, and √(a2 + 1 - 2a cos A). So a necessary and sufficient condition for the covering is 4 sin2A ≥ (a2 + 1 - 2a cos A), which reduces to a ≤ cos A + √3 sin A, since cos A ≤ a (the foot of the perpendicular from D onto AB must lie between A and B).
Problem 2
Prove that a tetrahedron with just one edge length greater than 1 has volume at most 1/8.
Solution
Let the tetrahedron be ABCD and assume that all edges except AB have length at most 1. The volume is the 1/3 x area BCD x height of A above BCD. The height is at most the height of A above CD, so we maximise the volume by taking the planes ACD and BCD to be perpendicular. If AC or AD is less than 1, then we can increase the altitude from A to CD whilst keeping BCD fixed by taking AC = AD = 1. A similar argument shows that we must have BC = BD = 1.
But the volume is also the 1/3 x area ABC x height of D above ABC, so we must adjust CD to maximise this height. We want the angle between planes ABC and ABD to be as close as possible to 90o. The angle increases with increasing CD until it becomes 90o. CMD is then a right-angled triangle. Now the angle ACB must be less than the angle between the planes ACD and BCD and hence < 90o, so angle ACM < 45o, so CM > 1/√2. Similarly DM. Hence when CMD = 90o we have CD > 1. Thus we maximise the height of D above ABC by taking CD = 1.
So BCD is equilateral with area (√3)/4. ACD is also equilateral with altitude (√3)/2. Since the planes ACD and BCD are perpendicular, that is also the height of A above BCD. So the volume is 1/3 x(√3)/4 x (√3)/2 = 1/8.
Problem A3
Let k, m, n be natural numbers such that m + k + 1 is a prime greater than n + 1. Let cs = s(s+1). Prove that:
(cm+1 - ck)(cm+2 - ck) ... (cm+n - ck)
is divisible by the product c1c2 ... cn.
Solution
The key is that ca - cb = (a - b)(a + b + 1). Hence the product (cm+1 - ck)(cm+2 - ck) ... (cm+n - ck) is the product of the n consecutive numbers (m - k + 1), ... , (m - k + n), times the product of the n consecutive numbers (m + k + 2), ... , (m + k + n + 1). The first product is just the binomial coefficient (m-k+n)Cn times n!, so it is divisible by n!. The second product is 1/(m + k + 1) x (m + k + 1)(m + k + 2) ... (m + k + n + 1) = 1/(m + k + 1) x (m+k+n+1)C(n+1) x (n+1)!. But m + k + 1 is a prime greater than n + 1, so it has no factors in common with (n+1)!, hence the second product is divisible by (n+1)!. Finally note that c1c2 ... cn= n! (n+1)!.
Problem B1
A0B0C0 and A1B1C1 are acute-angled triangles. Construct the triangle ABC with the largest possible area which is circumscribed about A0B0C0 (BC contains A0, CA contains B0, and AB contains C0) and similar to A1B1C1.
Solution
Take any triangle similar to A1B1C1 and circumscribing A0B0C0. For example, take an arbitrary line through A0 and then lines through B0 and C0 at the appropriate angles to the first line. Label the triangle's vertices X, Y, Z so that A0 lies on YZ, B0 on ZX, and C0 on XY. Now any circumscribed ABC (labeled with the same convention) must have C on the circle through A0, B0 and Z, because it has ∠C = ∠Z = ∠C1. Similarly it must have B on the circle through C0, A0 and Y, and it must have A on the circle through B0, C0 and X.
Consider the side AB. It passes through C0. Its length is twice the projection of the line joining the centers of the two circles onto AB (because each center projects onto the midpoint of the part of AB that is a chord of its circle). But this projection is maximum when it is parallel to the line joining the two centers. The area is maximised when AB is maximised (because all the triangles are similar), so we take AB parallel to the line joining the centers. [Note, in passing, that this proves that the other sides must also be parallel to the lines joining the respective centers and hence that the three centers form a triangle similar to A1B1C1.]
Problem B2
a1, ... , a8 are reals, not all zero. Let cn = a1n + a2n + ... + a8n for n = 1, 2, 3, ... . Given that an infinite number of cn are zero, find all n for which cn is zero.
Solution
Take |a1| ≥ |a2| ≥ ... ≥ |a8|. Suppose that |a1|, ... , |ar| are all equal and greater than |ar+1|. Then for sufficiently large n, we can ensure that |as|n < 1/8 |a1|n for s > r, and hence the sum of |as|n for all s > r is less than |a1|n. Hence r must be even with half of a1, ... , ar positive and half negative.
If that does not exhaust the ai, then in a similar way there must be an even number of ai with the next largest value of |ai|, with half positive and half negative, and so on. Thus we find that cn = 0 for all odd n.
Problem B3
In a sports contest a total of m medals were awarded over n days. On the first day one medal and 1/7 of the remaining medals were awarded. On the second day two medals and 1/7 of the remaining medals were awarded, and so on. On the last day, the remaining n medals were awarded. How many medals were awarded, and over how many days?
Solution
Let the number of medals remaining at the start of day r be mr. Then m1 = m, and 6(mk - k)/7 = mk+1 for k < n with mn = n.
After a little rearrangement, we find that m = 1 + 2(7/6) + 3(7/6)2 + ... + n(7/6)n-1. Summing, we get m = 36(1 - (n + 1)(7/6)n + n (7/6)n+1) = 36 + (n - 6)7n/6n-1. 6 and 7 are coprime, so 6n-1 must divide n - 6. But 6n-1 > n - 6, so n = 6 and m = 36.
Solutions are also available in: Samuel L Greitzer, International Mathematical Olympiads 1959-1977 , MAA 1978, and in István Reiman, International Mathematical Olympiad 1959-1999, ISBN 189-8855-48-X.
, MAA 1978, and in István Reiman, International Mathematical Olympiad 1959-1999, ISBN 189-8855-48-X.
 Labels:
IMO
Labels:
IMO



 Previous Article
Previous Article
