5th Iberoamerican Mathematical Olympiad Problems 1990

A1.  The function f is defined on the non-negative integers. f(2ⁿ - 1) = 0 for n = 0, 1, 2, ... . If m is not of the form 2ⁿ - 1, then f(m) = f(m+1) + 1. Show that f(n) + n = 2^k - 1 for some k, and find f(2¹⁹⁹⁰).

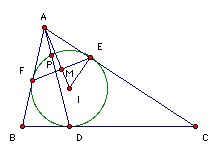
A2.  I is the incenter of the triangle ABC and the incircle touches BC, CA, AB at D, E, F respectively. AD meets the incircle again at P. M is the midpoint of EF. Show that PMID is cyclic (or the points are collinear).

A3.  f(x) = (x + b)² + c, where b and c are integers. If the prime p divides c, but p² does not divide c, show that f(n) is not divisible by p² for any integer n. If an odd prime q does not divide c, but divides f(n) for some n, show that for any r, we can find N such that q^r divides f(N).

B1.  The circle C has diameter AB. The tangent at B is T. For each point M (not equal to A) on C there is a circle C' which touches T and touches C at M. Find the point at which C' touches T and find the locus of the center of C' as M varies. Show that there is a circle orthogonal to all the circles C'.

B2.  A and B are opposite corners of an n x n board, divided into n² squares by lines parallel to the sides. In each square the diagonal parallel to AB is drawn, so that the board is divided into 2n² small triangles. The board has (n + 1)² nodes and large number of line segments, each of length 1 or √2. A piece moves from A to B along the line segments. It never moves along the same segment twice and its path includes exactly two sides of every small triangle on the board. For which n is this possible?

B3.  f(x) is a polynomial of degree 3 with rational coefficients. If its graph touches the x-axis, show that it has three rational roots. 

Solutions

Problem A1

The function f is defined on the non-negative integers. f(2ⁿ - 1) = 0 for n = 0, 1, 2, ... . If m is not of the form 2ⁿ - 1, then f(m) = f(m+1) + 1. Show that f(n) + n = 2^k - 1 for some k, and find f(2¹⁹⁹⁰).
Solution

We claim that if 2^m <= n < 2^m+1, then f(n) = 2^m+1 - n - 1. Put r = 2^m+1 - n. Then the claim follows by induction on r. Hence f(2¹⁹⁹⁰) = 2¹⁹⁹⁰ - 1.

Problem A2
I is the incenter of the triangle ABC and the incircle touches BC, CA, AB at D, E, F respectively. AD meets the incircle again at P. M is the midpoint of EF. Show that PMID is cyclic (or the points are collinear).
Solution

∠AEI = ∠AME = 90^o, so AEI and AME are similar. Hence AM/AE = AE/AI or AM·AI = AE². AE is tangent to the incircle, so AE2 = AP·AD. Hence AM·AI = AP·AD, so if P,M,I,D are not collinear, then they are cyclic.
Thanks to Johann Peter Gustav Lejeune Dirichlet

Problem A3
f(x) = (x + b)² + c, where b and c are integers. If the prime p divides c, but p² does not divide c, show that f(n) is not divisible by p² for any integer n. If an odd prime q does not divide c, but divides f(n) for some n, show that for any r, we can find N such that q^r divides f(N).
Solution
The first part is trivial. If p does not divide (x+b), then it does not divide (x+b)², so it does not divide (x+b)²+c. On the other hand, if p does divide x+b, then p² divides (x+b)², so p² does not divide (x+b)²+c.
For the second part, we use induction on r. For r = 1, we are given that q divides f(n). Now suppose that q^r divides f(N) for some N. If q^r+1 divides f(N), then we are done. So suppose q^r+1 does not divide f(N), so f(N) = q^rh where q does not divide h. We have f(N+kq^r) = f(N) + q^r(2N+2b)k = q^rh + q^r(2N+2b)k. Now q divides (N+b)²+c, and does not divide c, so it does not divide (N+b)² and hence does not divide N+b. It is odd, so it does not divide 2N+2b. Hence we can find k such that k(2N+2b) = -h mod q. Then we have q^r+1 divides f(N+kq^r), which completes the induction.

Problem B1
The circle C has diameter AB. The tangent at B is T. For each point M (not equal to A) on C there is a circle C' which touches T and touches C at M. Find the point at which C' touches T and find the locus of the center of C' as M varies. Show that there is a circle orthogonal to all the circles C'.
Answer
C' touches T at the intersection of T and the line AM
the locus of the center is a parabola vertex B
the circle center A radius AB is orthogonal to all circles C'
Solution

Let O be the center of C. Let the line AM meet T at N. Let the perpendicular to T at N meet the line OM at O'. Then ∠O'NM = ∠MAB (O'N parallel to AB, because both perpendicular to T) = ∠OMA (OM = OA) = ∠O'MN. So O'M = O'N. Hence O' is the center of C'.

Take B to be the origin and A to be the point (2a,0), so O is (a,0) and C has radius a. If O' is (x,y), then we require that O'O = x+a or (x-a)²+y² = (x+a)², or y² = 4ax, which is a parabola with vertex B and axis the x-axis.

Triangles AMB, ABN are similar (∠AMB = ∠ABN = 90^o), so AM/AB = AB/AN and hence AM·AN = AB². Now consider the circle center A radius AB. It must meet the circle C', because it contains the point M. Suppose it meets at X. Then AX² = AB² = AM·AN, so AX is tangent to C' and hence the circles are orthogonal. 

Problem B2

A and B are opposite corners of an n x n board, divided into n² squares by lines parallel to the sides. In each square the diagonal parallel to AB is drawn, so that the board is divided into 2n² small triangles. The board has (n + 1)² nodes and large number of line segments, each of length 1 or √2. A piece moves from A to B along the line segments. It never moves along the same segment twice and its path includes exactly two sides of every small triangle on the board. For which n is this possible?

Answer

n=2 only

Solution

The diagram above shows that n=2 is possible (the path is AHEFGHCDIHB). Now suppose n > 2.

Note that if X is any vertex except A or B, then an even number of segments with endpoint X must be in the path.

Let F be the bottom left-hand vertex. Two sides of the triangle EFG are in the path, so at least one of EF and FG is. But EF and EG are the only segments with endpoint F, so an even number of them must be in the path, so both are in the path. Hence, again considering EFG, EG is not in the path. Hence, considering EHG, EH and HG are in the path.

E has an even number of segments on the path, so CE is not on the path. Hence (considering CEH) CH is on the path. Similarly, GJ is not on the path and HJ is on the path. An even number of segments at H are on the path, so DH and HI are either both on the path or neither is on the path. But (considering DHI) at least one must be, so they both are. Hence DI is not, and CD is not.

Since n > 2, C is not the top left vertex. Considering MCD, MC and MD are both on the path. Considering DLI, DL is on the path. There must be an even number of segments at D, so DP is on the path. Hence MP is not. Now M cannot be the top left vertex (with n = 3) because then it should have an odd number of segments, whereas it would have two (MC and MD). So there must be a vertex N above M. Considering NMP, MN must be in the path. But now M has an odd number of segments. Contradiction. 

Problem B3

f(x) is a polynomial of degree 3 with rational coefficients. If its graph touches the x-axis, show that it has three rational roots.

Solution

Without loss of generality, f(x) = x³ - ax² + bx - c, where a, b, c are rational. Since the graph touches the x-axis, there is a repeated root, so we may take the roots to be h, h, k. Hence 2h + k = a, 2hk + k² = b, h²k = c. Hence a² - 3b = (h - k)². Put r = ±√(a² - 3b), where the sign is chosen so that h = a/3 + r/3, k = a/3 - 2r/3. We need to show that r is rational. If r is zero there is nothing to prove, so assume r is non-zero.

We have 9h² = 2a² - 3b + 2ar. Hence 27h²k = -2a³ + 9ab + (6b - 2a²)r. But 27h²k = 27c. So r = (27c + 2a³ - 9ab)/(2(3b - a²)). Note that 3b - 2a² is non-zero because r is non-zero. So r is a rational combination of a, b, c and hence is rational.