magnitude of rotation In a rotation, the amount that the preimage is turned about the center of rotation, measured in degrees from -180 (clockwise) to 180 (counterclockwise), +/- m<POP', where P' is the image of P under the rotation and O is its center.
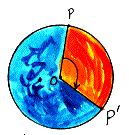 | Rotations, which are sometimes called turns, can also have magnitudes outside the range of -180 to 180 degrees, such as 720 degrees or -500 degrees. The thing you want to remember is that you are going around in a circle, and every circle has only 360 degrees. So a rotation of -500 degrees is really just one complete, clockwise, revolution of -360 and -140 degrees more. |
magnitude of size transformation In a size change, the factor by which the length of the preimage is changed, A'B'/AB , where A' and B' are the images of A and B under the transformation. Also called a size change factor or scale factor of size transformation.
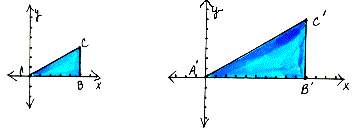 | The magnitude of this size transformation is two, because AB=5 units and A'B'=10. The lengths on the image A'B'C' are all two times larger than on the preimage ABC. |
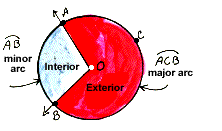 | NOTE: Three letters are used to identify major arcs. |
mapping An operation on a geometric figure by which each point gives rise to a unique image. A correspondence between two sets of points such that each point in the preimage set has a unique image, and each point in the image set has exactly one preimage. Also called a transformation.
mean A number that describes a set of other numbers. You get a mean, or average, as it is commonly called, by taking the sum of the numbers being examined and then dividing that sum by how many numbers were added.
For example: To find the mean, or average, of 10, 9, 8, and 5 this is what you would do:
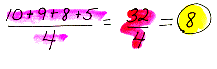
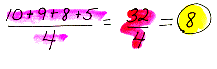
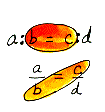 | Proportions used to always be written with colons on a straight line as you see at the top of our example. The word "means" meant "middle", thus the two numbers in the middle were called the means. It made perfect sense to those historical folks, but people today often wonder why b and c are called the means because today we usually write proportions as equal fractions with a horizontal fraction bar. *NOTE: a and d are called the extremes. This is because "extremes" meant "outside" and the a and d are on the outer sides of the horizontally written proportion. |
means-extremes property In any proportion, the product of the means equals the product of the extremes. Some people learn this as "cross products are equal in any proportion."
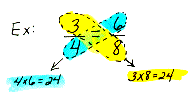
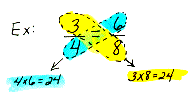
median of a triangle The segment connecting a vertex of the triangle to the midpoint of the opposite side.
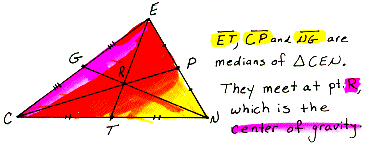  | Here we see all of the medians of triangle CEN. The spot where they intersect, pt R, is called the center of gravity, and is a perfect balance point for the triangle. You can prove this by cutting out the triangle and balancing it on the tip of a pin directly at point R. |
menu A list of options from which a user of a computer can select an operation for the computer to perform.
Mercator projection A two- dimensional map of the Earth's surface named for Gerhardus Mercator, the Flemish cartographer who first created it in 1569.
metric system of measurement A system of measurement based on the decimal system. Also called the international system of measurement.
mixed numeral A symbol consisting of a whole number with a fraction next to it, when written like this it means the numbers are being added.
mode The number which appears most often in a data set. The mode of the following data set is 6 : 15, 6, 2, 6, 42, 6.
It is possible to have more than one mode as in the set 1, 1, 3, 12, 4, 4. It is possible to have no mode if no values appear more than once as in the set 1, 2, 3, 4.
Multiplication of Fractions Property for all numbers a, b, c, and f with b and f not equal to 0:
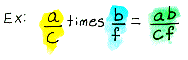 | Just multiply the numerators and then multiply the denominators. |
Multiplicative Identity Property of One For any number n:
n times 1 = n.
*We like to say that multiplying a number by one causes it to retain its identity.
n times 1 = n.
*We like to say that multiplying a number by one causes it to retain its identity.
multiplicative inverse The number by which a given number can be multiplied resulting in a product equal to 1. Also called reciprocal.
Mult-Rec Property of Division For any numbers a, and b, with b not equal to 0: a/b = a times 1/b. In words, to divide by a number is the same as multiplying by its reciprocal.
Ex: To divide by 2 gives the same answer as multiplying by 1/2. 24 divided by 2 = 12 and 24 times 1/2 = 12.
 Labels:
Math terms glossary
Labels:
Math terms glossary


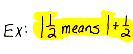
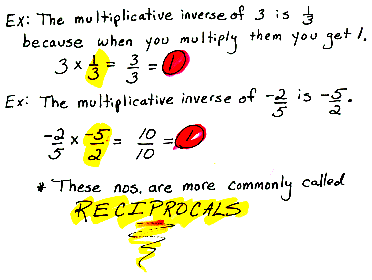
 Previous Article
Previous Article
