A1. Show that there are no integers m, n such that 3 n4 - m4 = 131.
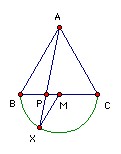
A2. ABC is equilateral. P and Q are points on BC such that BP = PQ = QC = BC/3. K is the semicircle on BC as diameter on the opposite side to A. The rays AP and AQ meet K at X and Y. Show that the arcs BX, XY and YX are all equal.
A3. The quartic x4 + (2a+1) x3 + (a-1)2x2 + bx + 4 factorises as p(x)(x2 + cx + d). The quadratic x2 + cx + d has two roots (real or complex) u and v such that p(u) = v and p(v) = u. Find all possible values of a and b.
B1. A graph has 6 points and 15 edges. Each edge is colored red or blue, so that there are no blue triangles. The number of red edges at each point is a, b, c, d, e, f. Show that (2a - 7)2 + (2b - 7)2 + ... + (2f - 7)2 < 55.
B2. Given a triangle ABC, take similar isosceles triangles PBC, QCA, RAB (with bases BC, CA, AB respectively, so that PB = PC etc), P on the same side of BC as A, Q on the opposite side of CA to B, and R on the opposite side of AB to C.Show that AQPR is a parallelogram. 

B3. N is the set of positive integers. M is the set of non-negative integers. f: N → M is a function such that f(10) = 0, f(n) = 0 if the last digit of n is 3, f(mn) = f(m) + f(n). Find f(1984) and f(1985).
Solutions
Problem A1
Show that there are no integers m, n such that 3 n4 - m4 = 131.
Solution
Any fourth power = 0 or 1 mod 5. Hence 3 n4 - m4 = 0, 4, 3 or 2 mod 5.
Problem A2
ABC is equilateral. P and Q are points on BC such that BP = PQ = QC = BC/3. K is the semicircle on BC as diameter on the opposite side to A. The rays AP and AQ meet K at X and Y. Show that the arcs BX, XY and YX are all equal.
Solution
Let M be the midpoint of BC. Consider triangles ABP and XMP. We have BP/MP = 2 = AB/XM and ∠P common. That is enough to make them similar. Hence ∠BMX = 60o. Similarly, ∠CMY = 60o, so the three arcs are equal.
Problem A3
The quartic x4 + (2a+1) x3 + (a-1)2x2 + bx + 4 factorises as p(x)(x2 + cx + d). The quadratic x2 + cx + d has two roots (real or complex) u and v such that p(u) = v and p(v) = u. Find all possible values of a and b.
Answer
(a,b) = (2,-14) or (-1,-2)
Solution
Suppose the other quadratic is x2 + ex + f. We have u2 + eu + f = v, v2 + ev + f = u. Subtracting gives u+v = -e - 1. Adding gives u2 + v2 + (e-1)(u+v) + 2f = 0. Substituting for u + v, we get (e+1)2 - 2uv - (e2-1) + 2f = 0, so uv = e + f + 1. Hence x2 + cx + d ≡ x2 + (e+1)x + e+f+1. Multiplying we get for the quartic x4 + (2e+1)x3 + (e2+2e+2f+1)x2 + (e2+2ef+e+f)x + f2+ef+f.
Comparing x3, a = e. Comparing x2, f = -2e. Comparing x, b = -3e2-e. Comparing the constant term, 2e2-2e = 4. So e = 2 or -1. Hence either a = 2, b = -14 or a = -1, b = -2.
Checking, we have in the first case x4 + 5x3 + x2 - 14x + 4 = (x2 + 2x - 4)(x2 + 3x - 1). The roots of the second quadratic are (-3 ±√13)/2. Substituting (-3+√13)/2 in the first quadratic we get 22/4 - (3/2)√13 -3 + √13 - 4 = (-3-√13)/2, which works. Similarly, substituting (-3-√13)/2 we get (-3+√13)/2. So the first case checks.
In the second case we have x4 - x3 + 4x2 - 2x + 4 = (x2 - x + 2)(x2 + 2). The roots of the second quadratic are ±i√2, i√2 gives -i√2 in the first and vice versa. So the second case works.
Problem B1
A graph has 6 points and 15 edges. Each edge is colored red or blue, so that there are no blue triangles. The number of red edges at each point is a, b, c, d, e, f. Show that (2a - 7)2 + (2b - 7)2 + ... + (2f - 7)2 < 55.
Solution
Note that (2a-7)2 = 49, 25, 9, 1, 1, 9 for a = 0, 1, 2, 3, 4, 5 (obviously a ≤ 5). Let A be the point with a edges, B the point with b edges etc. Suppose a = 0. Then there can be no other blue edges, for if BC is a blue edge, then ABC is a blue triangle. So the other points all have 4 red edges. So the sum is 49 + 5·1 < 55. So we can assume that none of a, b, ... , f are 0. Suppose a = 1. Suppose AB is red and AC, AD, AE, AF are blue. There can be no blue edges between any of C, D, E, F. So c, d, e, f = 3 or 4. Hence the sum is at most 25 + 25 + 1 + 1 + 1 + 1 < 55. Similarly if any other point has just one red edge. So we can assume all points have at least two red edges. But that means the sum is at most 5·9 = 45.
Problem B2
Given a triangle ABC, take similar isosceles triangles PBC, QCA, RAB (with bases BC, CA, AB respectively, so that PB = PC etc), P on the same side of BC as A, Q on the opposite side of CA to B, and R on the opposite side of AB to C.Show that AQPR is a parallelogram.
Solution
We show that RBP and QPC are congruent. It follows that AQ = QC = RP, and AR = RB = PQ, so AQPR is a parallelogram.
We start by showing that RBP and ABC are similar. Since RBA and PBC are similar, it follows that ∠RBA = ∠PBC and hence ∠RBP = ∠ABC. Also RB/AB = PB/BC. So RBP and ABC are similar. In the same way QPC and ABC are similar, so RBP and QPC are similar. But BP = PC, so they are congruent.
Problem B3
N is the set of positive integers. M is the set of non-negative integers. f: N → M is a function such that f(10) = 0, f(n) = 0 if the last digit of n is 3, f(mn) = f(m) + f(n). Find f(1984) and f(1985).
Answer
0, 0
Solution
0 = f(10) = f(5) + f(2) so f(5) = f(2) = 0. Hence also f(n) = 0 if no primes except 2 and 5 divide n. If n ends in the digit 1, then 3n ends in the digit 3, so 0 = f(3n) = f(3) + f(n), so f(n) = 0. If n ends in the digit 7, then 9n ends in the digit 3, so 0 = f(9n) = f(9) + f(n), so f(n) = 0. If n ends in the digit 9, then 7n ends in the digit 3, so again f(n) = 0. Given any n we may write n = bc, where no primes except 2 and 5 divide b, and c is not divisible by 2 or 5. So f(n) = f(b) + f(c) = 0.
Comment: This is almost a straight copy of British MO 1977/1.
Solutions are also available in Australian Mathematical Olympiads 1979-1995 by H Lausch and P J Taylor, ISBN 0858896451, published by Australian Mathematics Trust
by H Lausch and P J Taylor, ISBN 0858896451, published by Australian Mathematics Trust

 Previous Article
Previous Article
