A1. Find the smallest natural number with 6 as the last digit, such that if the final 6 is moved to the front of the number it is multiplied by 4.
A2. Find all real x satisfying: √(3 - x) - √(x + 1) > 1/2.
A3. The cube ABCDA'B'C'D' has upper face ABCD and lower face A'B'C'D' with A directly above A' and so on. The point x moves at constant speed along the perimeter of ABCD, and the point Y moves at the same speed along the perimeter of B'C'CB. X leaves A towards B at the same moment as Y leaves B' towards C'. What is the locus of the midpoint of XY?
B1. Find all real solutions to cos2x + cos22x + cos23x = 1.
B2. Given three distinct points A, B, C on a circle K, construct a point D on K, such that a circle can be inscribed in ABCD.
B3. The radius of the circumcircle of an isosceles triangle is R and the radius of its inscribed circle is r. Prove that the distance between the two centers is √(R(R - 2r)).
B4. Prove that a regular tetrahedron has five distinct spheres each tangent to its six extended edges. Conversely, prove that if a tetrahedron has five such spheres then it is regular.
Solutions
Problem A1
Find the smallest natural number with 6 as the last digit, such that if the final 6 is moved to the front of the number it is multiplied by 4.
Solution
We have 4(10n+6) = 6·10m + n, where n has m digits. So 13n + 8 = 2·10m. Hence n = 2n' and 13n' = 10m - 4. Dividing, we quickly find that the smallest n', m satisfying this are: n' = 7692, m = 5. Hence the answer is 153846.
Problem A2
Find all real x satisfying: √(3 - x) - √(x + 1) > 1/2.
Solution
It is easy to show that the inequality implies |x-1| > √31/8, so x > 1 + √31/8, or x < 1 - √31/8. But the converse is not true.
Indeed, we easily see that x > 1 implies the lhs < 0. Also care is needed to ensure that the expressions under the root signs are not negative, which implies -1 ≤ x ≤ 3. Putting this together, suggests the solution is -1 ≤ x < 1 - √31/8, which we can easily check.
Problem A3
The cube ABCDA'B'C'D' has upper face ABCD and lower face A'B'C'D' with A directly above A' and so on. The point x moves at constant speed along the perimeter of ABCD, and the point Y moves at the same speed along the perimeter of B'C'CB. X leaves A towards B at the same moment as Y leaves B' towards C'. What is the locus of the midpoint of XY?
Solution
Answer: the rhombus CUVW, where U is the center of ABCD, V is the center of ABB'A, and W is the center of BCC'B'.
Take rectangular coordinates with A as (0, 0, 0) and C' as (1, 1, 1). Let M be the midpoint of XY. Whilst X is on AB and Y on B'C', X is (x, 0, 0) and Y is (1, x, 1), so M is (x/2 + 1/2, x/2, 1/2) = x (1, 1/2, 1/2) + (1-x) (1/2, 0, 1/2) = x W + (1-x) V, so M traces out the line VW.
Whilst X is on BC and Y is on C'C, X is (1, x, 0) and Y is ( 1, 1, 1-x), so M is (1, x/2+1/2, 1/2 - x/2) = x (1, 1, 0) + (1-x) (1, 1/2, 1/2) = x C + (1-x) W, so M traces out the line WC.
Whilst X is on CD and Y is on CB, X is (1-x, 1, 0) and Y is (1, 1-x, 0), so M is (1-x/2, 1-x/2, 0) = x (1, 1, 0) + (1-x) (1/2, 1/2, 0) = x C + (1-x) U, so M traces out the line CU.
Whilst X is on DA and Y is on BB', X is (0, 1-x, 0) and Y is (1, 0, x), so M is (1/2, 1/2 - x/2, x/2) = x (1/2, 0, 1/2) + (1-x) (1/2, 1/2, 0) = x V + (1-x) U, so M traces out the line UV.
Problem B1
Find all real solutions to cos2x + cos22x + cos23x = 1.
Solution
Put c = cos x, and use cos3x = 4c3 - 3c, cos 2x = 2 c2 - 1. We find the equation given is equivalent to c = 0, c2 = 1/2 or c2 = 3/4. Hence x = π/2, 3π/2, π/4, 3π/4, π/6, 5π/6 or any multiple of π plus one of these.
Problem B2
Given three distinct points A, B, C on a circle K, construct a point D on K, such that a circle can be inscribed in ABCD.
Solution
 |  |
I be the center of the inscribed circle. Consider the quadrilateral ABCI. ∠BAI = 1/2 ∠BAD and ∠BCI = 1/2 ∠BCD, so ∠BAI + ∠BCI = 90o, since ABCD is cyclic. Hence ∠AIC = 270o - ∠ABC. So if we draw a circle through A and C such that for X points on the arc AC ∠AXC = 90o + ∠ABC, then the intersection of the circle with the angle bisector of ∠ABC gives the point I.
To draw this circle take the diameter AE. Then ∠CAE = 180o - ∠ACE - ∠AEC = 90o - ∠ABC. So we want AE to be tangent to the circle. Thus the center of the circle is on the perpendicular to AE through A and on the perpendicular bisector of AC.
To prove the construction possible we use the fact that a quadrilateral ABCD has an inscribed circle iff AB + CD = BC + AD. For D near C on the circumcircle of ABC we have AB + CD < BC + AD, whilst for D near A we have AB + CD > BC + AD, so as D moves continuously along the circumcircle there must be a point with equality. [Proof that the condition is sufficient: it is clearly necessary (use fact that tangents from a point are of equal length). So take a circle touching AB, BC and AD and let the other tangent from C (not BC) meet AD in D'. Then CD' - CD = AD' - AD, hence D'= D.]
Problem B3
The radius of the circumcircle of an isosceles triangle is R and the radius of its inscribed circle is r. Prove that the distance between the two centers is √(R(R - 2r)).
Solution
 | 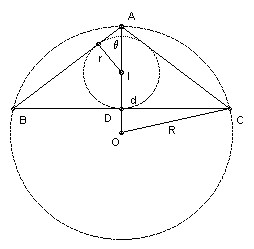 |
Let the triangle be ABC with AB = AC, let the incenter be I and the circumcenter O. Let the distance IO be d, taking d positive if O is closer to A than I, negative if I is closer. Let the ∠OAB be θ.
Then r = (R + d) sin θ, and r + d = R cos 2θ. It helps to draw a figure to check that this remains true for the various possible configurations. Using cos 2θ = 1 - 2 sin2θ, we find that (d + R + r)(d2 - R(R - 2r)) = 0. But OI < OA, so d is not - R - r. Hence result.
Comment.
This result is known as Euler's formula and is true for any triangle. Suppose two chords PQ and ST of a circle intersect at I. Then PIS and TIQ are similar, so PI·IQ = SI·IT. Take the special case when ST is perpendicular to OI, where O is the center of the circle, then SI·IT = SI2 = R2 - OI2, where R is the radius of the circle, so PI·IQ = R2 - OI2.
Now let O be the circumcenter, I the incenter of an arbitrary triangle ABC. Extend AI to meet the circumcircle again at D. Then by the above IO2 = R2 - AI·ID. If E is the foot of the perpendicular from I to AC, then AI = r/sin(A/2). We show that DI = DB. ∠DBI = ∠DBC + ∠CBI = ∠DAC + ∠DBI = A/2 + B/2. ∠DIB = ∠IAB + ∠IBA = A/2 + B/2. Hence ∠DBI = ∠DIB, so DI = DB, as claimed. Take F on the circle so that DF is a diameter, then ∠DFB = ∠DAB = A/2, so DB = 2R sin A/2. Thus IO2 = R2 - r/sin(A/2) 2R sin(A/2) = R2 - 2Rr.
Problem B4
Prove that a regular tetrahedron has five distinct spheres each tangent to its six extended edges. Conversely, prove that if a tetrahedron has five such spheres then it is regular.
Solution
First part is obvious. The wrong way to do the second part is to start looking for the locus of the center of a sphere which touches three edges. The key is to notice that the tangents to a sphere from a given point have the same length.
Let the tetrahedron be A1A2A3A4. Let S be the sphere inside the tetrahedron, S1 the tetrahedron opposite A1, and so on. Let the tangents to S from Ai have length ai. Then the side AiAj has length ai+aj. Now consider the tangents to S1 from A1. Their lengths are a1 + 2a2, a1 + 2a3, and a1 + 2a4. Hence a2 = a3 = a4. Similarly, considering S2, we have that a1 = a3 = a4.
Solutions are also available in: Samuel L Greitzer, International Mathematical Olympiads 1959-1977 , MAA 1978, and in István Reiman, International Mathematical Olympiad 1959-1999, ISBN 189-8855-48-X.
, MAA 1978, and in István Reiman, International Mathematical Olympiad 1959-1999, ISBN 189-8855-48-X.
 Labels:
IMO
Labels:
IMO




 Previous Article
Previous Article
