Amazing Number Facts No (part 2)

Here is a remarkable formula: f(n) = n²-n+41

f(1) = 1²-1+41 = 41 a prime number

f(2) = 2²-2+41 = 43 a prime number

f(3) = 3²-3+41 = 47 a prime number

f(4) = 4²-4+41 = 53 a prime number

 

How many prime numbers does this formula produce?

A formula that always produces prime numbers in this way has never been found. So just how good is this formula at producing primes? You may need a list of prime numbers to help when you do your calculations. Good luck!

The HARMONIC NUMBERS are:

H₁ = 1

H₂ = 1 + ¹/₂ = 1.5

H₃ = 1 + ¹/₂ + ¹/₃ = 1.8333 ...

H₄ = 1 + ¹/₂ + ¹/₃ + ¹/₄ = 2.08333 ...

So just how large is H_n?

You might like to check on a calculator that H₆₀ = 4.6798 ...

The 60th Prime Number is 281 and one 60th of 281 is 4.6833 ...

Is it just a coincidence that these answers are very close?

Calculate H₁₀₀ (15 minutes at most!) and then find one 100th of the 100th prime and be amazed!---

What is amazing about the number 21322314?

And what has it to do with the sequence:

1

11

21

1112

3112

211213

?

If you are completely confused then FIND OUT---

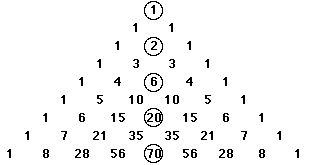
The factors of the central numbers in Pascal's Triangle follow a pattern:

1 = 1 x 1

2 = 2 x 1

6 = 3 x 2

20 = 4 x 5

70 = 5 x 14

etc

The numbers in the sequence 1, 1, 2, 5, 14 ... are called the Catalan Numbers.

What have they got to do with the Bubbles Investigation ?

Why don't you try the investigation to find out?!!

If you want to know why Catalan Numbers are important try:

LINK1 or LINK2 or LINK3 or LINK4---

¹/₇ = 0.142857142857142857142...with repeating cycle (142857).

Suppose the cycle is reversed to give 0.758241758241758241758... or .(758241)

What fraction is this? It is ⁶⁹/₉₁. But ¹/₇ can be written ¹³/₉₁.

¹/₁₃ = 0.(076923) so what fraction is 0.(329670) ? It's ³⁰/₉₁. But ¹/₁₃ = ⁷/₉₁.

This amazing pattern is worth exploring further! For example:

¹/₉₁= ? Now reverse the cycle to get ^?/₉₁

²/₉₁= ? Now reverse the cycle to get ^?/₉₁

and so on ...---

Some formulae produce lots of primes one after the other...

n²-n+2=2 for n=1

n²-n+3=3,5 for n=1,2

n²-n+5=5,7,11,17 for n=1,2,3,4

n²-n+11=11,13,17,23,31,41,53,67,81,101 for n=1,2,...10

Try n²-n+17 for yourself (see a list of prime numbers if needed)

Now look at Amazing Number Fact No 11

Can you find other Prime-Rich Formulae?---

We all know and love the Triangular Numbers 1, 3, 6, 10, 15, 21 ...

and we all know and love the Square numbers 1, 4, 9, 16, 25 ...

but how often have we wondered if the only Square Triangular number is 1 ?

A little calculation might produce the next example.

A very much longer calculation may produce another.

However a change of lifestyle would be needed to find 41616, the fourth example.

And a lifetime may well be too short to find 1413721 the fifth example. Consider the sequence 1, 6, 35, 204 ...

obtained from the recurrence relation u_n = 6u_n-1 - u_n-2 with u₁=1 and u₂= 6 .

Now square each term of this sequence.

Isn't that amazing!!??---

7 is a prime number

73 is a prime number

739 is a prime number

7393 is a prime number

73939 is a prime number

739391 is a prime number

7393913 is a prime number

73939133 is a prime number

73939133 is an amazing prime number...

...if you keep chopping the end digit off you still get a prime.

It is the largest known prime with this property.

What's the largest one you can find in The List?---

A Pythagorean Triple (a,b,c) is a set of three whole numbers which can form the sides of a right-angled triangle. So a² + b² = c².

You are familiar with the example (3,4,5) giving 3² + 4² = 5².

Multiples also work ... (6,8,10) and (9,12,15) etc.

Not so familiar is the fact that there are 18 triples (ignoring multiples) with the two smaller numbers less than 100. Here they are:

3 , 4 , 5	12 , 35 , 37	33 , 56 , 65
5 , 12 , 13	13 , 84 , 85	36 , 77 , 85
7 , 24 ,25	16 , 63 , 65	39 , 80 , 89
8 , 15 , 17	20 , 21, 29	48 , 55 , 73
9 , 40 , 41	20 , 99 , 101	60 , 91, 109
11 , 60 , 61	28 , 45 , 53	65 , 72 , 97

There are some remarkable patterns among these numbers. Can you find any?---

What is special about the number 1395 ?

Well 1395 = 15 x 93.

It is called a VAMPIRE number with fangs 15 and 93.

Another example is 1435 = 35 x 41 with the two fangs 35 and 41.

If you know the fangs, for example 30 and 51, its easy to find the vampire...

...but if you meet the vampire, for example 1827, can you find its fangs?

And how easy is it to spot a vampire hiding among innocent numbers?

For instance which among 2155, 2170 and 2187 is the vampire?

Vampire numbers have an even number of digits with their two fangs sharing half that number between them.

There are exactly seven 4-digit vampire numbers. If you worked through the examples above you should now know five of them. Can you find the other two? One is less than 1395 and the other ...?

Some large vampire numbers have a spare pair of fangs...

125460 = 204 x 615 = 246 x 510

or even two spare pairs ...

13078260 = 1620 x 8073 = 1863 x 7020 = 2070 x 6318

Now that is amazing!