A1. Find all possible values for the sum of the digits of a square.
A2. n > 1. Find all solutions in real numbers x1, x2, ... , xn+1 all at least 1 such that: (1) x11/2 + x21/3 + x31/4 + ... + xn1/(n+1) = n xn+11/2; and (2) (x1 + x2 + ... + xn)/n = xn+1.
A3. L and L' are two perpendicular lines not in the same plane. AA' is perpendicular to both lines, where A belongs to L and A' belongs to L'. S is the sphere with diameter AA'. For which points P on S can we find points X on L and X' on L' such that XX' touches S at P?
B1. ABCD is an n x n board. We call a diagonal row of cells a positive diagonal if it is parallel to AC. How many coins must be placed on an n x n board such that every cell either has a coin or is in the same row, column or positive diagonal as a coin?
B2. The incircle of the triangle ABC touches the sides BC, CA, AB at D, E, F respectively. AD meets the circle again at X and AX = XD. BX meets the circle again at Y and CX meets the circle again at Z. Show that EY = FZ.
B3. f is a function defined on the positive integers with positive integer values. Use f m(n) to mean f(f( ... f(n) ....)) = n where f is taken m times, so that f 2(n) = f(f(n)), for example. Find the largest possible 0 < k < 1 such that for some function f, we have f m(n) ≠ n for m = 1, 2, ... , [kn], but f m(n) = n for some m (which may depend on n).
Solutions
Problem A1
Find all possible values for the sum of the digits of a square.
Solution
Answer: any non-negative integer = 0, 1, 4 or 7 mod 9.
02 = 0, (±1)2 = 1, (±2)2 = 4, (±3)2 = 0, (±4)2 = 7 mod 9, so the condition is necessary.
We exhibit squares which give these values.
0 mod 9. Obviously 02 = 0. We have 92 = 81, 992 = 9801 and in general 9...92 = (10n - 1)2 = 102n - 2.10n + 1 = 9...980...01, with digit sum 9n.
1 mod 9. Obviously 12 = 1 with digit sum 1, and 82 = 64 with digit sum 10. We also have 982 = 9604, 9982 = 996004, and in general 9...982 = (10n - 2)2 = 102n - 4.10n + 4 = 9...960...04, with digit sum 9n+1.
4 mod 9 Obviously 22 = 4 with digit sum 4, and 72 = 49 with digit sum 13. Also 972 = 9409 with digit sum 22, 9972 = 994009 with digit sum 31, and in general 9...972 = (10n - 3)2 = 102n - 6.10n + 9 = 9...940...09, with digit sum 9n+4.
7 mod 9 Obviously 42 = 16, with digit sum 7. Also 952 = 9025, digit sum 16, 9952 = 990025 with digit sum 25, and in general 9...952 = (10n - 5)2 = 102n - 10n+1 + 25 = 9...90...025, with digit sum 9n-2.
Problem A2
Find all solutions in real numbers x1, x2, ... , xn+1 all at least 1 such that: (1) x11/2 + x21/3 + x31/4 + ... + xn1/(n+1) = n xn+11/2; and (2) (x1 + x2 + ... + xn)/n = xn+1.
Answer
The only solution is the obvious, all xi = 1.
Solution
By Cauchy-Schwartz, (∑ xi1/2)2 ≤ (∑ 1)(&sum xi), with equality iff all xi equal. In other words, if we put xn+1 = (x1 + x2 + ... + xn)/n, then ∑ xi1/2 ≤ n xn+11/2. But since all xi ≥ 1, we have x11/2 + x21/3 + x31/4 + ... + xn1/(n+1) ≤ ∑ xi1/2 with equality iff x2 = x3 = ... = xn = 1. Hence x11/2 + x21/3 + x31/4 + ... + xn1/(n+1) ≤ xn+11/2 with equality iff all xi = 1.
Problem B1
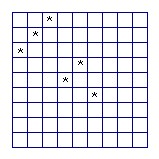
ABCD is an n x n board. We call a diagonal row of cells a positive diagonal if it is parallel to AC. How many coins must be placed on an n x n board such that every cell either has a coin or is in the same row, column or positive diagonal as a coin?
Answer
smallest integer ≥ (2n-1)/3
[so 2m-1 for n = 3m-1, 2m for n = 3m, 2m+1 for n = 3m+1]
[so 2m-1 for n = 3m-1, 2m for n = 3m, 2m+1 for n = 3m+1]
Solution
There must be at least n-k rows without a coin and at least n-k columns without a coin. Let r1, r2, ... , rn-k be cells in the top row without a coin which are also in a column without a coin. Let r1, c2, c3, ... , cn-k be cells in the first column without a coin which are also in a row without a coin. Each of the 2n-2k-1 ri and cj are on a different positive diagonal, so we must have k ≥ 2n-2k-1 and hence k ≥ (2n-1)/3.
Let (i,j) denote the cell in row i, col j. For n = 3m-1, put coins in (m,1), (m-1,2), (m-2,3), ... , (1,m) and in (2m-1,m+1), (2m-2,m+2), ... , (m+1,2m-1). It is easy to check that this works. For n = 3m, put an additional coin in (2m,2m), it is easy to check that works. For n = 3m+1 we can use the same arrangement as for 3m+2.
Problem B3
f is a function defined on the positive integers with positive integer values. Use f m(n) to mean f(f( ... f(n) ....)) = n where f is taken m times, so that f 2(n) = f(f(n)), for example. Find the largest possible 0 < k < 1 such that for some function f, we have f m(n) ≠ n for m = 1, 2, ... , [kn], but f m(n) = n for some m (which may depend on n).
Answer
we can get k arbitrarily close to 1
Solution
The basic idea is to take a block of integers m+1, m+2, ... , M and to define f(m+1) = m+2, f(m+2) = m+3, ... , f(M-1) = M, f(M) = m+1. Then for any integer h in the block we have fn(h) ≠ h for n = 1, 2, ... , M-m-1 and fM-m(h) = h. Note that the ratio (M-m)/h is worst (smallest) for h = M.
For example, take the first block to be 1, 2, ... , N, the second block to be N+1, ... , N2, the third block, N2+1, ... , N3 and so on. Then for any integer n we have fm(n) ≠ n for m < kn where k = 1 - 1/N.
 Labels:
Iberoamerican Mathematical Olympiad
Labels:
Iberoamerican Mathematical Olympiad

 Previous Article
Previous Article
